겉보기에는 단순해 보이지만, 원뿔은 평면도형과 입체도형의 개념을 자연스럽게 연결해 주는 중요한 역할을 합니다.
특히 전개도, 겉넓이, 부피 개념은 이후 배우게 될 원기둥이나 구의 학습으로 이어지기 때문에 기초를 정확히 이해하는 것이 중요합니다.
이번 글에서는 원뿔의 정의부터 구성 요소, 전개도, 겉넓이와 부피까지 차근차근 정리해보겠습니다.
원뿔이란 무엇입니까?
원뿔은 밑면이 원인 입체도형입니다.
원 하나와, 그 원의 둘레 위에 있는 모든 점을 하나의 점(꼭짓점)과 연결하여 만든 도형을 원뿔이라고 합니다.
실생활에서는 다음과 같은 물건에서 원뿔을 쉽게 찾아볼 수 있습니다.

- 아이스크림 콘
- 깔때기
- 종이로 만든 뾰족한 모자
- 교통 안전용 고깔
이처럼 원뿔은 우리 주변에서 자주 접하지만, 수학적으로는 구조를 정확히 구분해 이해해야 하는 도형입니다.
원뿔을 이루는 기본 요소
원뿔에는 반드시 알아야 할 네 가지 중요한 요소가 있습니다.
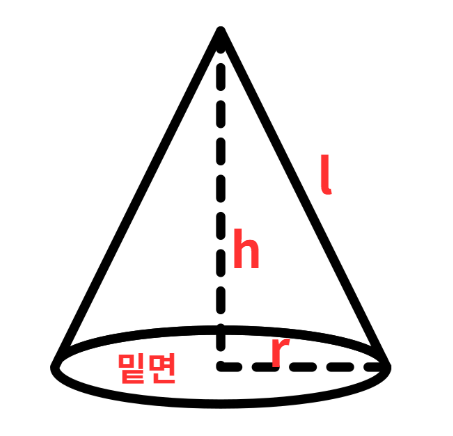
1. 밑면
원뿔의 아래쪽에 있는 원 모양의 면입니다.
밑면의 반지름은 보통 r로 나타내며, 밑면의 넓이는 πr²입니다.
2. 꼭짓점
원뿔의 가장 위쪽에 있는 뾰족한 점입니다.
원뿔의 모든 옆면은 이 꼭짓점으로 모입니다.
3. 높이(h)
꼭짓점에서 밑면으로 수직으로 내린 선분의 길이를 높이라고 합니다.
반드시 직각이어야 하며, 옆으로 기울어진 길이는 높이가 아닙니다.
학생들이 가장 많이 헷갈리는 부분 중 하나입니다.
4. 모선(l)
꼭짓점과 밑면의 원 위 한 점을 연결한 선분입니다.
원뿔을 옆에서 보았을 때 보이는 기울어진 면의 길이를 의미하며, 높이와는 다른 개념입니다.
이 네 가지 요소를 정확히 구분하면 이후의 계산이 훨씬 쉬워집니다.
높이, 반지름, 모선의 관계
원뿔을 한쪽으로 잘라 단면을 보면 직각삼각형이 만들어집니다.
이때 다음과 같은 관계가 성립합니다.
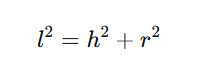
여기서
- 모선(l)은 직각삼각형의 빗변에 해당하고
- 높이(h)와 반지름(r)은 서로 직각을 이루는 두 변입니다.
즉, 원뿔에서는 피타고라스 정리가 그대로 적용됩니다.
이 관계를 이해하면 모선이나 높이가 주어졌을 때 나머지 값을 쉽게 구할 수 있습니다.
원뿔의 전개도 이해하기
원뿔을 잘라 평면 위에 펼치면 전개도가 됩니다.
원뿔의 전개도는 다음 두 부분으로 이루어져 있습니다.
- 밑면에 해당하는 원 1개
- 옆면에 해당하는 부채꼴 1개
이때 중요한 점은 다음과 같습니다.
- 부채꼴의 반지름은 모선(l)입니다.
- 부채꼴의 호의 길이는 밑면 원의 둘레(2πr)와 같습니다.
즉, 원뿔의 옆면은 삼각형이 아니라 둥글게 펼쳐진 부채꼴 모양입니다.
이 구조를 이해하면 겉넓이 공식이 자연스럽게 연결됩니다.
원뿔의 겉넓이
원뿔의 겉넓이는 다음 두 넓이의 합입니다.
- 밑면의 넓이
- 옆면의 넓이
이를 공식으로 나타내면 다음과 같습니다.
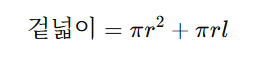
여기서
- πr²는 밑면(원)의 넓이이며
- πrl은 옆면(부채꼴)의 넓이입니다.
옆면의 넓이가 πrl이 되는 이유는 전개도에서 부채꼴의 넓이를 계산한 결과입니다.
원뿔의 부피
원뿔의 부피는 다음 공식으로 구합니다.
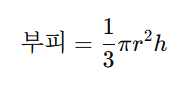
이 공식에서 반드시 기억해야 할 점은
같은 밑면과 높이를 가진 원기둥의 부피의 1/3이라는 것입니다.
실제로 같은 크기의 원기둥에 원뿔 3개를 채우면 정확히 가득 차게 됩니다.
이 성질을 통해 원뿔의 부피 공식이 만들어졌습니다.
예제로 정리해보기
밑면의 반지름이 3cm, 높이가 4cm인 원뿔이 있다고 가정합니다.
1) 모선의 길이
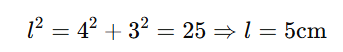
2) 부피
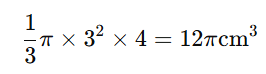
3) 겉넓이
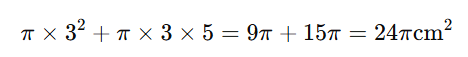
단계별로 계산 과정을 나누어 보면 공식의 의미가 더욱 분명해집니다.
원뿔 학습에서 중요한 포인트
- 높이와 모선을 명확히 구분해야 합니다.
- 전개도를 통해 옆면의 구조를 이해해야 합니다.
- 부피는 ‘원기둥의 1/3’이라는 개념으로 접근하는 것이 좋습니다.
- 공식 암기보다 구조 이해가 우선입니다.
원뿔은 단순히 계산만 하는 도형이 아니라,
입체도형의 구조를 이해하는 데 핵심이 되는 도형입니다.
마무리
원뿔은 초등 고학년부터 중학교 과정까지 반복적으로 등장하는 입체도형입니다.
처음 배울 때 구조와 개념을 정확히 잡아두면 이후의 도형 학습이 훨씬 수월해집니다.
전개도를 직접 그려보거나 종이로 원뿔을 만들어보는 활동도
원뿔을 이해하는 데 큰 도움이 됩니다.