쉽게 이해하는 1보다 작은 소수·큰 소수·크기 비교
초등 3학년 수학에서는 처음으로 분수와 소수를 배우기 시작합니다.
이 단원은 앞으로 배우게 될 비·비율, 백분율(%), 소수 계산, 도형 넓이 계산 등과 연결되기 때문에 정말 중요한 단원입니다.
하지만 많은 아이들이 처음 보는 ‘분수 기호(½, ⅓, ¾)’나
소수(0.1, 0.3, 2.3 같은 수)를 어려워합니다.
그래서 오늘은
아이들이 이 단원을 쉽게 이해할 수 있도록
그림을 떠올리며 공부할 수 있는 방식으로 자세히 설명해드리겠습니다.
1️⃣ 분수란 무엇일까요?
분수는 전체를 똑같이 나누었을 때 그중 일부를 나타내는 수입니다.
예를 들어, 피자를 생각해봅시다.
✔ 전체를 똑같이 2조각으로 나눈 뒤, 그중 1조각을 먹었어요
그러면 그 먹은 조각을 1/2(이분의 일)이라고 씁니다.
아이들은 이 개념이 ‘부분을 나타내는 표현’이라는 점을 이해해야 합니다.

✔ 전체를 4조각으로 나누었을 때 3조각을 색칠
이때 색칠한 부분은 3/4(사분의 삼)입니다.
여기서 중요한 점은
분모(아래 숫자)는 전체를 몇 조각으로 나누었는지,
분자(위 숫자)는 그중 몇 조각을 가졌는지
라는 의미입니다.
이 개념을 정확히 알면 분수가 매우 쉽습니다.

2️⃣ 단위분수란 무엇일까요?
단위분수는 분자가 1인 분수입니다.
예:
1/2, 1/3, 1/4 …
왜 단위분수가 중요할까요?
단위분수는 전체를 더 많이 나누면 조각 크기가 더 작아진다는 사실을 이해하는 데 큰 도움을 줍니다.
✔ 예를 들어
- 피자를 2조각 낸 것 중 1조각 → 큰 조각
- 피자를 4조각 낸 것 중 1조각 → 더 작은 조각
- 피자를 8조각 낸 것 중 1조각 → 더욱 작음
따라서 분모가 클수록 조각 크기는 작아집니다.
아이들이 가장 많이 하는 실수는
“숫자가 크니까 1/8이 1/4보다 크다”라고 생각하는 것입니다.
하지만 8조각 중 1조각이 더 작습니다.
이 개념이 자연스럽게 잡히면 분수 비교는 쉽게 해결됩니다.
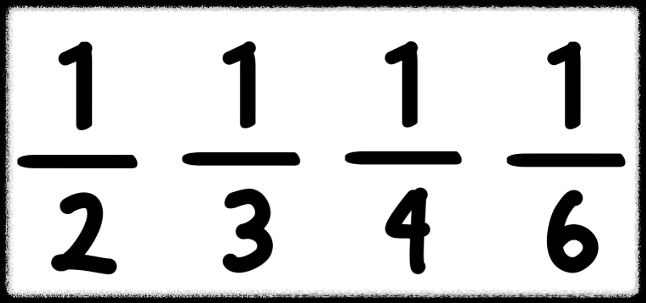
3️⃣ 분수의 크기 비교
3학년에서 배우는 분수 비교는 두 가지 경우뿐입니다.
(1) 분모가 같은 분수 비교
예: 3/5와 4/5 비교하기
분모가 같으면
→ 분자가 큰 쪽이 큰 분수입니다.
5등분한 조각의 크기는 모두 같기 때문에,
몇 조각을 차지하느냐가 크기를 결정합니다.
그래서 4/5가 3/5보다 큽니다.
(2) 분자가 같은 분수 비교
예: 1/3과 1/5 비교하기
1조각씩 가진 것은 같지만
전체를 나눈 횟수가 다르죠?
- 3등분한 조각은 크고
- 5등분한 조각은 더 작습니다
따라서
1/3 > 1/5
이해 포인트는 단 하나입니다.
전체를 많이 나눌수록 조각은 작아진다.
이 사실을 이해하는 순간
분수 비교는 완벽하게 해결됩니다.
4️⃣ 소수란 무엇일까요?
소수는 “점(.)이 있는 수”라고만 기억하면 안 됩니다.
소수의 본질은 전체를 10조각, 100조각 등으로 나누었을 때 어느 정도를 나타내는 수입니다.
예:
1/10 → 0.1
3/10 → 0.3
9/10 → 0.9
이처럼 분모가 10인 분수는 소수로 아주 쉽게 바꿀 수 있습니다.
✔ 소수에서 소수점 아래 첫째 자리는 ‘십분의 자리’입니다
0.1 → 십분의 1
0.5 → 십분의 5
0.7 → 십분의 7
왜 ‘십분의’일까요?
전체를 10등분했기 때문입니다.
▶ 아이들이 자주 혼동하는 부분
0.1과 0.01의 차이를 모르는 경우가 많습니다.
- 0.1 = 십분의 1
- 0.01 = 백분의 1
따라서
0.1이 0.01보다 10배나 큽니다.
이 개념이 잡히면 소수 크기 비교가 훨씬 쉬워집니다.
5️⃣ 1보다 작은 소수: 0.1, 0.2, 0.3 …
1보다 작은 소수는
전체 중에서 아주 작은 양을 나타내는 표현입니다.
예: 0.3은 십분의 3이기 때문에
전체를 10조각 냈을 때 그중 3조각에 해당합니다.
교과서 그림처럼, 10칸을 가진 막대를 그려
3칸을 칠하면 0.3이 되는 방식입니다.
6️⃣ 1보다 큰 소수: 2.3, 3.7 …
1보다 큰 소수는
자연수와 소수가 합쳐진 형태입니다.
예: 2.3은
→ 자연수 2
→ 십분의 3(0.3)을 더한 값입니다.
따라서 수직선에서
2와 3 사이 중간쯤에 표시됩니다.
아이들이 가장 어려워하는 이유는
“2.3이 2보다 큰데도 3보다는 작다”
라는 상대적 위치를 이해하기 어렵기 때문입니다.
이때 수직선 그림이 매우 효과적입니다.
7️⃣ 소수의 크기 비교
소수 비교는 아래 두 단계만 알면 됩니다.
(1) 소수점 왼쪽(자연수) 비교
자연수가 크면 무조건 큰 수입니다.
예: 3.2 > 2.9
(2) 소수점 오른쪽 비교
자연수가 같을 때는
십분의 자리 숫자부터 비교합니다.
예:
1.5와 1.8 비교
→ 5 < 8 이므로 1.5 < 1.8
여기서 중요한 점은
‘십분의 자리 → 백분의 자리’ 순으로 비교한다는 것입니다.
▶ 아이들이 흔히 하는 실수
❌ 1.50은 1.5보다 크다
→ 둘 다 같습니다.
❌ 0.9보다 0.10이 크다
→ 실제로는 0.9가 훨씬 큽니다.
왜냐면
- 0.9 = 십분의 9
- 0.10 = 십분의 1
이기 때문입니다.
8️⃣ 분수와 소수를 연결하면 이해력이 2배가 됩니다
1/10 = 0.1
2/10 = 0.2
3/10 = 0.3
이렇게 분수와 소수를 연결해주는 순간
아이들은 숫자의 크기를 그림 없이도 추론할 수 있게 됩니다.
특히 3학년에서 배운 분수 개념이
5학년의 소수 계산, 6학년의 분수·소수 혼합 계산으로 자연스럽게 이어집니다.
3학년 ‘분수와 소수’는 수학의 기초 체력을 만드는 핵심 단원입니다
이 단원은 단순히 기호를 읽는 것이 아니라
✔ 전체를 나누는 개념
✔ 양을 비교하는 능력
✔ 수의 위치를 이해하는 사고력
을 키우는 중요한 과정입니다.
분수와 소수가 정확히 잡히면
이후 수학 학습이 훨씬 수월해지고
아이 스스로 문제를 이해하는 힘이 커집니다.