다각형에서 대각선을 구하는 방법은 초등에서 꼭 한번 생각해봐야 하는 중요한 개념입니다.
하지만 “공식 n(n−3)/2”만 외우면 금방 잊어버리게 됩니다.
그래서 오늘은 공식이 어떻게 만들어지는지를 아주 쉽게,
초등 눈높이에 맞춰 차근차근 설명해 드리겠습니다.

1️⃣ 대각선이 뭔지 먼저 알아야 해요
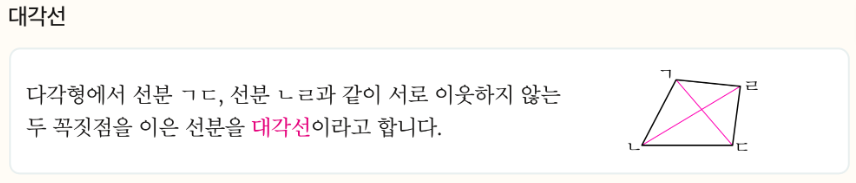
대각선은 서로 이웃하지 않은 두 점을 연결한 선입니다.
예를 들어 사각형을 떠올려 볼까요?
옆에 있는 점끼리 잇는 건 변입니다.
옆에 있지 않은 점 둘을 잇는 것이 대각선입니다.
즉, “옆에 있는 점은 제외하고, 떨어진 점끼리 연결해야” 대각선이 됩니다.
2️⃣ 모든 점을 연결하면 선분이 몇 개 나올까?
다각형에는 꼭짓점(점)이 n개 있습니다.
선분 하나를 만들려면 두 점이 필요합니다.
그럼 “n개 중에 두 점을 뽑는 방법”이 바로 전체 선분의 개수입니다.
점 2개를 고르는 방법은
👉 n(n−1)/2 개입니다.
이 안에는
변
대각선
둘 다 들어 있습니다.
그래서 여기서 “변”을 빼면 대각선만 구할 수 있어요.
3️⃣ 변의 개수는 항상 n개!
삼각형은 3개
사각형은 4개
오각형은 5개…
즉, n각형의 변은 항상 n개입니다.
그래서
전체 선분에서 변을 빼면 대각선이 됩니다.

4️⃣ 그래서 대각선은 이렇게 계산합니다
전체 선분 − 변
= n(n−1)/2 − n
이걸 정리하면
👉 n(n−3)/2
바로 이 공식이 나옵니다.
이렇게 보면,
“뜬금없이 나온 공식이 아니라, 자연스럽게 만들어진 공식”이라는 걸 알 수 있어요.

5️⃣ 그런데… ‘n−3’은 왜 나올까?
이 부분이 아이들이 가장 궁금해하는 부분입니다.
쉽게 그림을 떠올리며 생각해볼게요.
- 하나의 꼭짓점(점)을 잡습니다.
그 점과 연결할 수 있는 점은 몇 개일까요? - 자기 자신은 연결할 수 없음
- 양 옆의 두 점과 연결하면 변이 됨
- 나머지 점들은 모두 대각선을 만들 수 있음
그래서
👉 연결 가능한 점 = n − 3
즉, “한 점에서 나오는 대각선이 n−3개”라는 뜻입니다.
그런데 n개의 점이 있으니까
👉 전체는 n(n−3)
하지만 한 선분은 두 번 세게 되죠?
(A에서 C, C에서 A 둘 다 같은 선)
그래서 2로 나눕니다.
👉 n(n−3)/2
아까와 똑같은 공식이 다시 나왔습니다.
6️⃣ 실제 예로 확인해볼까요?
◼ 사각형(n=4)
4(4−3)/2 = 4×1/2 = 2
✔ 사각형 대각선 2개 맞아요!
◼ 오각형(n=5)
5(5−3)/2 = 5×2/2 = 5
✔ 오각형 대각선 5개 맞아요!
◼ 육각형(n=6)
6×3/2 = 9
✔ 육각형 대각선 9개 정확합니다!
예시로 확인해보면 “공식이 정말 맞구나!” 싶은 느낌이 듭니다.
7️⃣ 초등에서 이 공식을 왜 배울까?
대각선 공식은 단순히 “대각선이 몇 개냐”를 구하는 것이 아닙니다.
여기에는 중요한 수학적 사고가 들어 있습니다.
✔ 전체 중에서 필요한 것만 골라내기
전체 선분에서 변을 빼는 과정
✔ 중복 계산을 조심하기
A→C와 C→A는 같은 대각선이므로 나누기 2를 하는 과정
✔ 점과 선 사이의 관계 이해
한 점에서 몇 개의 선이 나오는지 생각하는 과정
이것은 나중에 배우는
- 조합
- 경우의 수
- 도형의 구조
모두와 깊이 연결됩니다.
※ 쉽게 정리하면 이렇게 됩니다
대각선 수 =
① 전체 선분 수(n(n−1)/2)에서
② 변의 수(n)를 빼고
③ 정리한 식이
👉 n(n−3)/2
또는
대각선 수 =
① 한 점에서 만들 수 있는 대각선 수(n−3) × n
② 중복이므로 나누기 2
👉 n(n−3)/2
두 방식 모두 같은 식이 됩니다.
🟣 마무리
초등에서 대각선 공식을 그냥 외우는 것은 쉽지 않습니다.
하지만 이렇게 “왜인지”를 이해하고 나면
시험 때, 중학교 때, 혹은 더 어려운 도형 문제를 만났을 때
자연스럽게 떠오르는 ‘이해된 지식’이 됩니다.
대각선 공식은
그 자체가 하나의 완성된 수학 이야기이며,
논리적으로 생각하는 힘을 키워주는 좋은 예시입니다.