1. 선의 관계를 이해하기 전에
초등학교 4학년 수학에서는 ‘점, 선, 각’의 개념이 한 단계 더 깊어집니다.
그중에서도 ‘선과 선 사이의 관계’를 이해하는 것이 가장 중요하지요.
우리가 평소에 보는 모든 도형, 예를 들어 직사각형, 정사각형, 삼각형, 사다리꼴 등은
‘선이 어떻게 만나느냐’, ‘어떤 각도로 교차하느냐’에 따라 이름이 달라집니다.
그래서 이번 단원에서는 두 선이 서로 어떤 관계를 맺는지를 배우는데,
그 대표적인 관계가 바로 수직과 평행입니다.
2. 수직이란 무엇일까?
‘수직’이라는 말은 ‘곧게 아래로 떨어진다’는 뜻에서 왔습니다.
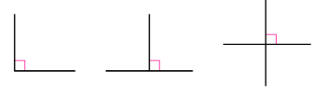
그래서 수직은 한 선이 다른 선과 직각(90도) 을 이루며 만나는 관계를 말합니다.
즉, 두 선이 만나서 직각을 만들면 그 두 선은 서로 수직이다라고 합니다.
직각은 ‘네모난 모서리’의 각도를 뜻하지요.
예를 들어 책의 모서리, 칠판의 네 귀퉁이, 문틀의 모양을 보면
모두 직각으로 되어 있습니다.
이처럼 직각을 이루는 두 선이 바로 수직 관계입니다.
🧭 수직의 예시
- 교실의 벽과 바닥은 서로 수직입니다.
- 문짝의 한쪽 변과 바닥도 수직입니다.
- 수직 방향으로 떨어지는 빗방울, 그리고 땅과의 관계도 수직입니다.
- 수학 공책의 가로줄과 세로줄이 서로 수직으로 교차되어 있습니다.
3. 수직선 그리는 방법
수직 관계를 이해했다면 이제 직접 그려볼 차례입니다.
초등학교에서는 자로 수직선을 그리는 방법을 익히게 됩니다.
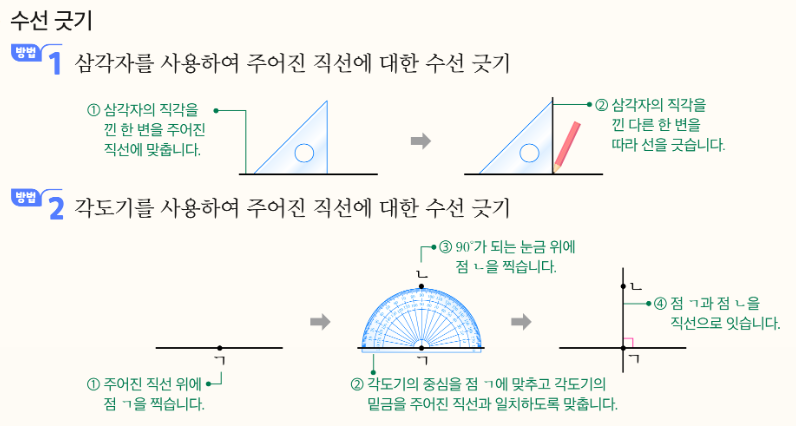
수직선을 그릴 때는 ‘자’와 ‘삼각자(직각자)’를 함께 사용합니다.
🧩 수직선을 그리는 순서
1️⃣ 기준이 되는 선을 한 줄 그립니다.
예를 들어, 종이에 가로선을 하나 긋습니다.
2️⃣ 삼각자의 직각 부분을 기준선에 바짝 붙입니다.
삼각자에는 직각(ㄱ 모양) 부분이 있지요.
그 부분을 기준선에 꼭 붙여야 합니다.
3️⃣ 삼각자를 움직이지 않고, 다른 쪽에 자를 밀착시킨 상태로 선을 긋습니다.
그렇게 하면 기준선과 새로 그린 선이 직각으로 교차합니다.
4️⃣ 두 선이 만나서 네모난 각을 이루면,
그 두 선은 서로 수직입니다.
💡 Tip:
수직을 확인할 때는 직각자나 삼각자의 모서리를 대보면 됩니다.
만약 그 모서리에 딱 맞게 선이 만난다면, 그건 바로 수직 관계입니다.
4. 평행이란 무엇일까?
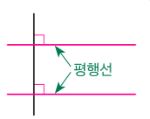
‘평행’이란 두 선이 서로 만나지 않고 나란히 이어지는 관계를 말합니다.
아무리 길게 그어도 절대로 만나지 않는 선, 그것이 평행선입니다.
즉, 두 선의 간격이 항상 같고, 끝까지 나란히 이어지는 관계이지요.
🧭 평행의 예시
공책의 가로줄들은 서로 평행입니다.
철길의 두 레일도 평행 관계입니다.
건물의 층을 구분하는 천장선과 바닥선도 평행입니다.
운동장의 달리기 트랙 라인도 서로 평행하게 나란히 이어져 있습니다.
이처럼 평행은 “나란히, 그러나 절대 만나지 않는 관계”입니다.
5. 평행선 그리는 방법
평행선을 그릴 때도 자와 삼각자를 함께 사용합니다.
수직선과 다르게, 이번에는 기준선과 같은 방향으로 나란히 그려야 합니다.
🧩 평행선을 그리는 순서
1️⃣ 종이에 기준선 하나를 긋습니다.
이 선은 평행을 만들 기준이 됩니다.
2️⃣ 삼각자의 한쪽 변을 기준선에 바짝 붙입니다.
3️⃣ 삼각자를 움직이지 않은 상태에서,
다른 자를 삼각자 옆에 붙여 고정합니다.
4️⃣ 삼각자를 고정된 자를 따라 위나 아래로 미끄러뜨립니다.
5️⃣ 삼각자를 새 위치에서 선을 그으면,
처음 선과 서로 만나지 않고 같은 방향으로 나란한 선,
즉 평행선이 완성됩니다.

💡 Tip:
삼각자의 한 변을 기준선에 붙인 채 움직이면
어떤 위치에서 선을 그어도 그 두 선은 반드시 평행하게 됩니다.
이것이 자와 삼각자를 이용해 평행선을 그리는 원리입니다.
6. 수직과 평행의 차이점
두 선의 관계를 구분할 때 가장 중요한 것은
“만나는가, 만나지 않는가” 그리고 “각의 크기”입니다.
- 수직: 두 선이 만나서 직각(90도) 을 이루는 관계입니다.
- 평행: 두 선이 절대 만나지 않고, 항상 같은 간격으로 나란한 관계입니다.
즉, 수직은 ‘만나면서 각을 이루는 선’,
평행은 ‘만나지 않고 일정한 간격을 유지하는 선’입니다.
이 둘은 완전히 반대되는 개념이지만, 도형 속에서는 함께 존재하기도 합니다.
예를 들어 직사각형의 경우를 보세요.
위쪽 변과 아래쪽 변은 서로 평행입니다.
왼쪽 변과 오른쪽 변도 서로 평행입니다.
그리고 가로 변과 세로 변은 서로 수직 관계입니다.
이렇게 한 도형 안에서도 수직과 평행이 함께 등장하는 것이지요.
7. 평행선 사이의 거리란?
평행선은 서로 만나지 않기 때문에,
그 사이의 간격(거리)은 언제나 같습니다.
이것이 평행선의 가장 중요한 성질입니다.
예를 들어 철길을 생각해 보세요.
두 레일은 출발점부터 도착점까지 나란히 이어집니다.
만약 레일 사이의 간격이 조금이라도 좁아지거나 넓어지면,
기차는 탈선하게 되겠지요.
따라서 평행선 사이의 거리는 항상 일정해야 합니다.
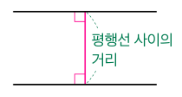
📏 평행선 사이 거리 재는 방법
평행선 사이의 거리를 잴 때는 수직선을 이용합니다.
두 평행선 사이의 가장 짧은 거리는
그 두 선에 수직으로 만나는 선의 길이입니다.
즉, 평행선 사이의 거리란
한 선에서 다른 선까지 직각 방향으로 잰 거리를 말합니다.
만약 비스듬하게 잰다면,
실제 거리보다 길게 나오기 때문에 정확하지 않습니다.
그래서 평행선 사이의 거리를 잴 때는
언제나 수직으로 내린 선분의 길이를 사용합니다.
8. 수직과 평행의 관계
이제 중요한 부분입니다.
수직과 평행은 서로 반대되는 개념이지만,
서로 관계를 맺고 작용합니다.
어떤 선에 수직인 선이 두 개 있으면,
그 두 선은 서로 평행입니다.
예를 들어, 바닥선에 수직으로 서 있는 두 개의 기둥을 상상해 보세요.
두 기둥은 바닥과는 수직이지만,
기둥끼리는 서로 나란히 서 있으므로 평행입니다.
즉, 같은 선에 수직인 두 선은 평행하다는 중요한 성질이 있습니다.
🔹 정리하자면
1️⃣ 두 선이 직각을 이루면 수직이다.
2️⃣ 두 선이 만나지 않고 나란히 있으면 평행이다.
3️⃣ 같은 선에 수직인 두 선은 서로 평행이다.
4️⃣ 평행선 사이의 거리는 언제나 같다.
5️⃣ 평행선 사이의 거리는 수직선으로 잰 거리가 정확하다.
9. 생활 속에서 찾는 수직과 평행
우리 주변에는 수직과 평행이 숨어 있는 곳이 아주 많습니다.
- 건물의 벽과 바닥: 수직
- 책장의 선반들: 평행
- 도로의 중앙선과 갓길선: 평행
- 신호등 기둥과 땅: 수직
- 운동장의 선: 서로 평행
- 칠판의 모서리: 수직
이처럼 세상은 수직과 평행으로 만들어졌다고 해도 과언이 아닙니다.
아이들이 실제로 주변을 관찰하며 “이건 수직, 저건 평행!” 하며 찾아보면
수학이 훨씬 더 흥미롭게 느껴질 것입니다.
🌟 마무리하며
초등학교 4학년의 수직과 평행 단원은
단순히 선을 그리는 기술이 아니라 세상을 바라보는 수학의 눈을 여는 과정입니다.
수직은 만나는 선, 평행은 나란한 선이라는 간단한 개념에서 출발하지만,
이 개념이 모여 사각형, 삼각형, 입체도형까지 이어집니다.
직각 자로 수직을 재고, 자와 삼각자로 평행을 그리는 과정 속에서
아이들은 도형의 질서를 이해하고 공간 감각을 기르게 됩니다.
결국, 수직과 평행은
“선과 선이 만드는 세상의 규칙”을 발견하는 첫걸음입니다.