사각형 단원에는 직사각형, 정사각형, 마름모, 평행사변형, 사다리꼴이 등장합니다.
이 다섯 가지 도형은 모두 네 개의 변으로 이루어져 있지만,
변의 길이나 각의 모양, 평행 여부에 따라 서로 다른 특징을 가지고 있습니다.
하나씩 차근차근 비교해 보겠습니다.
🔹 직사각형
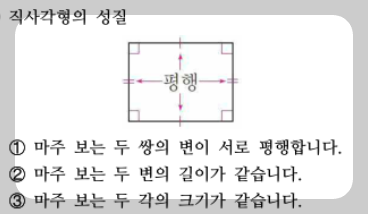
직사각형은 네 각이 모두 직각이고, 마주 보는 두 쌍의 변이 서로 평행한 도형입니다.
마주 보는 변의 길이는 서로 같으며, 대각선 두 개의 길이도 같습니다.
또한 대각선이 서로 교차하면서 반으로 나누어지는 성질을 가지고 있습니다.
즉, 직사각형은 “반듯한 모양의 네모”로, 변의 길이는 짝을 이루어 같고 각이 모두 네모꼴입니다.
대칭으로는 두 번 접었을 때 완전히 겹쳐지는 축대칭이 두 개,
돌려도 같은 모양이 되는 회전 대칭은 두 번 존재합니다.
🔹 정사각형
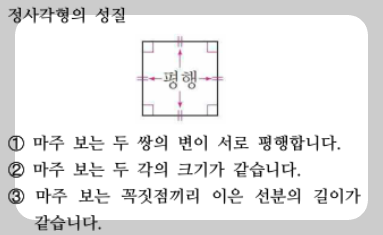
정사각형은 직사각형보다 더 특별한 사각형입니다.
직사각형처럼 네 각이 모두 직각이면서, 마름모처럼 네 변의 길이도 모두 같습니다.
따라서 정사각형은 직사각형과 마름모의 성질을 동시에 가지고 있습니다.
대각선은 서로 같은 길이이며, 서로 직각으로 교차하고, 교차점에서 정확히 반으로 나뉩니다.
이 대칭성 덕분에 정사각형은 사각형 중에서 가장 규칙적인 도형이라 할 수 있습니다.
정사각형은 네 번 돌려도 같은 모양이 되는 회전 대칭 네 번,
접었을 때 완전히 겹치는 축대칭 네 개를 가지고 있습니다.
그래서 대칭성이 가장 뛰어난 도형이라고 할 수 있습니다.
🔹 마름모

마름모는 네 변의 길이가 모두 같지만, 각이 모두 직각은 아닙니다.
즉, 정사각형처럼 변은 같지만 모양은 약간 기울어진 형태입니다.
그래서 정사각형이 반듯한 네모라면, 마름모는 살짝 기울어진 네모라고 생각하면 이해하기 쉽습니다.
마름모는 마주 보는 두 각의 크기가 서로 같고, 마주 보는 두 변이 평행합니다.
즉, 평행사변형의 성질을 가지고 있다고 할 수 있습니다.
또한 두 대각선은 서로 직각으로 만나며, 교차점에서 서로를 반으로 나눕니다.
대칭성은 정사각형보다 조금 적지만, 여전히 대칭선이 두 개 있습니다.
돌려도 같은 모양이 되는 회전 대칭도 두 번 있습니다.
요약하자면, 마름모는 “네 변이 모두 같지만 각이 직각이 아닌 평행사변형”입니다.
🔹 평행사변형

평행사변형은 사각형 중에서 가장 기본적인 모양입니다.
이 도형은 이름 그대로 서로 마주 보는 두 쌍의 변이 평행합니다.
즉, 위아래 변이 평행하고, 좌우 변도 평행하지요.
마주 보는 변의 길이가 같고, 마주 보는 각의 크기도 같습니다.
대각선이 교차할 때 서로를 반으로 나누지만, 길이는 서로 다를 수 있습니다.
직사각형, 마름모, 정사각형 모두 사실상 평행사변형의 특별한 형태라고 할 수 있습니다.
직사각형은 평행사변형 중에서 네 각이 직각인 경우이고,
마름모는 네 변이 같은 경우,
정사각형은 네 변이 같고 네 각이 모두 직각인 경우입니다.
평행사변형은 중심을 기준으로 돌리면 두 번 같은 모양이 되는 회전 대칭 두 번의 성질이 있습니다.
하지만 축대칭은 존재하지 않아, 종이로 접으면 완전히 겹쳐지지는 않습니다.
🔹 사다리꼴
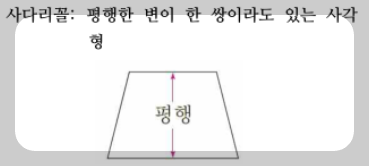
사다리꼴은 다른 사각형들과 달리 단 한 쌍의 변만 평행한 도형입니다.
즉, 위쪽과 아래쪽 변은 평행하지만, 양쪽의 변은 평행하지 않고 서로 만나게 됩니다.
이 평행한 두 변을 ‘밑변’이라 하고, 두 밑변 사이의 거리를 ‘높이’라고 합니다.
사다리꼴은 한 쌍만 평행하므로 모양이 조금 불안정해 보일 수 있지만,
그래서 오히려 다양한 형태를 만들어낼 수 있습니다.
예를 들어, 한쪽 변이 밑변과 직각으로 만나는 직사다리꼴,
평행하지 않은 두 변의 길이가 같고 대칭으로 접을 수 있는 이등변사다리꼴,
그리고 모든 변의 길이가 다르고 대칭이 없는 일반사다리꼴이 있습니다.
사다리꼴은 다른 도형들과 달리 평행이 한 쌍뿐이기 때문에
대각선의 길이가 서로 다르거나 교차점이 중앙이 아닐 수도 있습니다.
대칭성은 일부 이등변사다리꼴에서만 존재하며, 축대칭이 하나 있는 정도입니다.
🔸 다섯 도형의 차이를 한눈에 이해하기
이제 다섯 가지 도형을 성질 중심으로 정리해보면 다음과 같습니다.
- 직사각형은 각이 모두 직각이고, 마주보는 변이 평행하며 같은 길이입니다.
- 정사각형은 직사각형과 마름모의 성질을 모두 가진 도형으로, 네 변이 같고 네 각이 직각입니다.
- 마름모는 네 변이 모두 같고, 각이 직각이 아닌 평행사변형입니다.
- 평행사변형은 두 쌍의 변이 평행하고, 마주보는 변과 각이 서로 같습니다.
- 사다리꼴은 한 쌍의 변만 평행하며, 모양에 따라 여러 가지 형태로 나뉩니다.
요약하자면,
- 직사각형·정사각형·마름모·평행사변형은 평행한 변이 두 쌍 있는 사각형,
- 사다리꼴은 한 쌍만 평행한 사각형입니다.
- 그리고 이 중 정사각형은 대칭성이 가장 완벽하고,
- 사다리꼴은 평행이 한 쌍뿐이라 가장 자유로운 모양을 가집니다.

마무리하며
사각형 단원은 단순히 도형 이름을 외우는 것이 아니라,
도형의 모양, 각, 평행, 변의 길이 관계를 관찰하고 구분하는 것이 핵심입니다.
아이들이 자로 변의 길이를 재보고, 종이를 접어 대칭선을 찾아보고,
직각자를 대어 각의 크기를 확인해보는 활동을 해보면
이 다섯 가지 도형의 차이가 자연스럽게 눈에 들어옵니다.
정사각형과 직사각형, 마름모와 평행사변형처럼 겉으로 비슷해 보이는 도형도
직각의 유무, 변의 길이의 차이, 평행 관계를 구분하면 완전히 다른 도형임을 알 수 있습니다.
결국 이 단원은 도형을 눈으로 보고, 손으로 확인하며, 머리로 구분하는 학습입니다.
사각형의 세계를 이해하면 이후 5학년에서 배우게 될 ‘넓이’ 단원에서도 훨씬 쉽게 개념을 이어갈 수 있습니다.