Ⅰ. 비례란 무엇일까?
수학에서 비례란 “두 비가 같을 때의 관계”를 말합니다.
예를 들어 장성이와 해법이가 사탕을 가지고 있을 때,
장성이:해법이 = 2:3이고,
다른 상황에서도 두 사람의 비가 4:6이라면,
이건 두 비가 같은 관계를 유지하고 있다는 뜻이에요.
이처럼 두 비가 서로 같은 관계를 가지면,
그걸 비례한다고 말합니다.
두 비가 서로 같으면 비례한다.
비례한다는 건 ‘비의 관계가 일정하다’는 뜻이에요.
이제 이 개념을 바탕으로 비례식을 배워봅시다.
Ⅱ. 비례식이란 무엇인가?
① 비례식의 뜻
비례식은 두 개의 비가 서로 같다는 것을 나타내는 식이에요.
예를 들어
2:3 = 4:6
이게 바로 비례식입니다.
왼쪽의 비 2:3을 계산하면 2 ÷ 3 = 0.666…,
오른쪽의 비 4:6을 계산해도 4 ÷ 6 = 0.666…
두 결과가 같죠?
그래서 이건 “비례한다”고 할 수 있습니다.
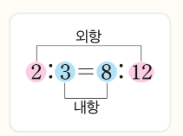
② 비례식의 네 가지 수
비례식에는 항상 네 개의 수가 등장합니다.
예를 들어
2:3 = 4:6
이면,
2는 첫째항, 3은 둘째항, 4는 셋째항, 6은 넷째항이에요.
비례식은 네 수가 일정한 규칙을 가질 때만 성립합니다.
그 규칙을 비례식의 성질이라고 합니다.
Ⅲ. 비례식의 성질

① 곱으로 비교하는 성질
비례식의 가장 중요한 성질은 다음과 같습니다.
첫째항 × 넷째항 = 둘째항 × 셋째항
이걸 비례식의 성질이라고 불러요.
예를 들어 2:3 = 4:6에서
2 × 6 = 12,
3 × 4 = 12
양쪽이 같죠?
그래서 이 비례식은 참입니다.
이 성질은 비례식을 풀 때 아주 유용하게 쓰입니다.
모르는 수가 하나 있어도 나머지를 이용해 계산할 수 있기 때문이에요.
② 비례식으로 미지수 구하기
예를 들어 3:x = 6:12라는 비례식이 있다고 해봅시다.
여기서 x가 무엇인지 구하려면
비례식의 성질을 이용해 곱으로 바꿔요.
3 × 12 = 6 × x
36 = 6x
x = 6
이렇게 쉽게 구할 수 있습니다.
비례식의 성질은 문제를 간단히 바꾸어 생각할 수 있게 해주는 도구랍니다.
Ⅳ. 비례식은 어디에 쓰일까?
비례식은 일상생활의 여러 곳에서 쓰입니다.
단순히 숫자 계산뿐 아니라,
요리, 지도, 속력, 도형 문제 등 다양한 상황에서 사용됩니다.
요리할 때
쿠키 반죽의 밀가루와 설탕 비가 4:1이라면,
밀가루를 8컵 썼을 때 설탕은 몇 컵일까요?
비례식으로 세워보면
4:1 = 8:x
비례식의 성질을 이용하면
4×x = 1×8 → x = 2
즉, 설탕은 2컵이에요.
지도에서 거리 계산할 때
지도에서 1cm가 실제 거리 5km를 의미할 때,
지도에서 두 도시 사이가 3cm라면 실제 거리는 얼마일까요?
1:5 = 3:x
1×x = 5×3 → x = 15
즉, 실제 거리는 15km입니다.
속력 계산
자동차가 2시간 동안 100km를 달렸다면,
1시간 동안 가는 거리는?
2:100 = 1:x
2×x = 1×100 → x = 50
즉, 속력은 1시간에 50km입니다.
비례식은 이렇게 생활 속 비율 관계를 계산할 때 매우 유용합니다.
Ⅴ. 비례식의 다양한 형태
비례식은 한 가지 형태만 있는 게 아니에요.
여러 상황에 따라 모양이 조금씩 달라집니다.
기본형
a:b = c:d
가장 기본적인 형태입니다.
교차형
a:c = b:d
비교하려는 위치에 따라 이렇게 변형되기도 합니다.
연속비례식
a:b = b:c
이건 특별한 비례식으로,
둘째항이 양쪽에 공통으로 들어갑니다.
이걸 연비라고 부릅니다.
예를 들어 2:4 = 4:8이면,
중간항인 4가 양쪽에 겹쳐서 들어가죠.
이걸 ‘연속비례’라고 합니다.
Ⅵ. 비례배분이란 무엇일까?
① 비례배분의 뜻
비례배분은 비의 관계에 따라 어떤 양을 나누는 방법이에요.
쉽게 말하면,
“정해진 비율대로 공평하게 나누는 것”입니다.
예를 들어 장성이와 해법이가 사탕 20개를
1:3의 비로 나눈다면,
장성이가 1, 해법이가 3의 비율로 나누어 가지게 됩니다.

② 비례배분의 원리
비례배분을 하려면
1️⃣ 비의 합을 구하고
2️⃣ 전체 양을 비의 합으로 나눈 뒤
3️⃣ 각자의 비만큼 곱해주면 됩니다.
예를 들어 1:3으로 20개를 나눈다면,
비의 합은 1+3=4
1부분은 20 ÷ 4 = 5
따라서
장성이: 5×1 = 5개
해법이: 5×3 = 15개
이렇게 나누면 비가 1:3으로 딱 맞아요.
예시 ① 용돈 나누기
엄마가 24,000원을 두 아이에게 2:1 비로 주기로 했어요.
비의 합은 2+1=3
한 부분은 24,000 ÷ 3 = 8,000
따라서
큰아이는 8,000×2 = 16,000원
작은아이는 8,000×1 = 8,000원
이렇게 나누면 16,000:8,000 = 2:1로 비례합니다.
예시 ② 문제로 생각해보기
세 친구가 6시간 동안 함께 일해서 60,000원을 받았어요.
그런데 일한 시간이 각각
2시간, 3시간, 1시간이라면
시간의 비는 2:3:1입니다.
비의 합은 6
한 부분은 60,000 ÷ 6 = 10,000
따라서
첫째 친구: 2×10,000 = 20,000원
둘째 친구: 3×10,000 = 30,000원
셋째 친구: 1×10,000 = 10,000원
이렇게 나누면 비례배분이 완성됩니다.
Ⅶ. 반비례의 개념도 알아두자
비례에는 정비례와 반비례가 있습니다.
정비례: 한쪽이 커질수록 다른 쪽도 커지는 관계
예) 시간과 거리 — 오래 달릴수록 더 먼 거리
반비례: 한쪽이 커질수록 다른 쪽은 작아지는 관계
예) 인원수와 일하는 시간 — 사람이 많을수록 걸리는 시간은 짧아짐
정비례는 두 비가 일정하게 증가하고,
반비례는 한쪽이 커질 때 다른 쪽이 줄어드는 관계입니다.
이 구분을 알면 비례문제를 더 잘 이해할 수 있습니다.
Ⅷ. 비례식과 비례배분의 차이 정리
비례식은 두 비가 같다는 관계를 보여주는 식이고,
비례배분은 그 비를 이용해 어떤 양을 나누는 방법이에요.
쉽게 말해,
비례식은 관계를 보여주는 ‘식’,
비례배분은 그 관계로 ‘나누는 계산’입니다.
예를 들어,
4:6 = 2:3 → 비례식
12개의 사탕을 1:3으로 나눈다 → 비례배분
비례식이 비례배분의 기초가 된다고 보면 됩니다.
Ⅸ. 실생활 속 비례의 예
비례는 생각보다 우리 주변에 아주 많습니다.
요리:
비율대로 재료를 넣지 않으면 맛이 달라집니다.
레시피의 기본은 비례예요.
지도:
축척은 실제 거리와 지도 거리의 비례 관계입니다.
그림 그리기:
인물의 키와 얼굴 크기를 일정한 비율로 그리면 자연스럽게 보입니다.
모형 만들기:
실제 물체를 작게 줄이거나 키울 때도 비례를 유지해야 해요.
금융·경제:
이익, 투자 비율, 세금 계산 등에서도 비례식이 자주 쓰입니다.
Ⅹ. 한 줄 정리
- 비례식: 두 비가 같다는 것을 나타내는 식이에요.
(예: 2:3 = 4:6) - 비례식의 성질: 첫째항×넷째항 = 둘째항×셋째항
- 비례배분: 비의 관계에 따라 어떤 양을 나누는 방법이에요.
(예: 1:3으로 20개를 나누면 5개와 15개로 나뉘어요.)
비례식은 ‘관계’,
비례배분은 ‘활용’이에요.
둘은 친구처럼 붙어 다니며,
하나를 알면 다른 하나도 쉽게 배울 수 있습니다.
Ⅺ. 마무리 — 비례는 세상을 이해하는 수학의 언어
비례식과 비례배분은 단순히 계산법이 아니라
세상 속에서 공평함과 균형을 이해하는 수학의 언어입니다.
공정하게 나누고, 정확하게 비교하고,
모양과 크기를 일정하게 유지하는 모든 일의 바탕에 비례가 있습니다.
그래서 비례를 잘 이해하면
수학뿐 아니라 생활 속 문제를 훨씬 논리적으로 해결할 수 있습니다.