초등 수학에서 학생들이 가장 헷갈려 하는 단원 중 하나가 바로 ‘분수와 소수의 크기 비교’입니다.
처음에는 분수끼리, 소수끼리 비교하는 건 비교적 쉽지만, 분수와 소수가 섞여 있으면 어떻게 비교해야 할지 막막해하는 경우가 많습니다.
오늘은 그 핵심 개념과 함께 분수를 소수로, 소수를 분수로 바꿔서 비교하는 방법을 자세히 살펴보겠습니다.
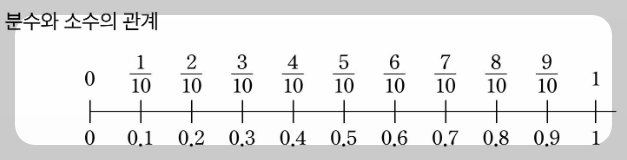
1️⃣ 분수와 소수의 의미 다시 보기
먼저, 분수와 소수가 무엇을 나타내는지 이해하는 것이 중요합니다.
분수는 전체를 일정한 수로 나눈 뒤, 그중 일부를 나타내는 수입니다.
예를 들어 1/2는 하나를 둘로 나눈 것 중 한 부분을 의미합니다.
소수는 1보다 작은 수를 십진법으로 나타낸 것입니다.
예를 들어 0.5는 1을 10으로 나눈 것 중 5개를 의미합니다.
즉, 분수와 소수는 같은 양을 다른 방식으로 표현하는 방법일 뿐입니다.
1/2와 0.5는 같은 수를 나타내는 것이죠.
2️⃣ 왜 분수와 소수를 비교해야 할까?
실생활에서는 두 형태가 함께 등장하는 경우가 많습니다.
예를 들어, 한 조각이 1/4인 피자와 0.3리터의 주스를 비교해야 할 때처럼요.
아이들이 수학을 공부할 때도, 시험에서 “1/4과 0.3 중 어느 쪽이 더 큰가요?”와 같은 문제가 자주 등장합니다.
이럴 때 단순히 감으로 비교하면 안 되고, 같은 형태로 바꿔서 비교해야 합니다.
즉, 분수를 소수로 바꾸거나, 소수를 분수로 바꾸는 과정이 필요합니다.
3️⃣ 분수를 소수로 바꾸는 방법
분수를 소수로 바꾸려면 분자 ÷ 분모를 계산하면 됩니다.
분수는 ‘나눗셈’을 뜻하기 때문입니다.
예시를 통해 살펴보겠습니다.
1/2 = 1 ÷ 2 = 0.5
1/4 = 1 ÷ 4 = 0.25
3/5 = 3 ÷ 5 = 0.6
이처럼 분자를 분모로 나누면, 소수로 바뀝니다.
단, 나눠도 나눠도 끝나지 않는 경우가 있습니다.
예를 들어 1 ÷ 3 = 0.333…처럼 무한소수가 나오는 경우인데, 이런 경우에는 일정 자리에서 반올림하여 표현합니다.
예를 들어 0.333… ≈ 0.33 또는 0.333으로 나타낼 수 있습니다.

4️⃣ 소수를 분수로 바꾸는 방법
이번엔 반대로 소수를 분수로 바꾸는 방법을 알아봅시다.
소수는 10분의 1, 100분의 1, 1000분의 1 단위로 나누어져 있으므로
소수점 아래 자리 수를 이용해 분모를 정할 수 있습니다.
0.5 = 5/10 = 1/2
0.25 = 25/100 = 1/4
0.6 = 6/10 = 3/5
즉, 소수점 아래 한 자리 → 10분의 1,
소수점 아래 두 자리 → 100분의 1,
소수점 아래 세 자리 → 1000분의 1로 보면 됩니다.
그리고 기약분수로 줄이면 가장 간단한 형태가 됩니다.

5️⃣ 크기 비교의 기본 원리
이제 분수와 소수를 비교하는 방법을 정리해보겠습니다.

① 분수를 소수로 바꿔서 비교하기
가장 흔하게 사용하는 방법입니다.
분수를 소수로 바꿔서 두 소수를 나란히 놓고 비교하면 됩니다.
예를 들어,
1/2과 0.4를 비교할 때 → 1/2 = 0.5
즉, 0.5 > 0.4 → 1/2이 더 큽니다.
② 소수를 분수로 바꿔서 비교하기
소수보다 분수 계산이 더 익숙하다면, 반대로 바꿔도 됩니다.
예를 들어,
0.6과 2/3을 비교할 때 → 0.6 = 3/5
3/5과 2/3을 비교하려면 통분을 해야 합니다.
3/5 = 9/15, 2/3 = 10/15
따라서 10/15 > 9/15, 즉 2/3이 더 큽니다.
6️⃣ 분수를 소수로 바꿔 비교하는 과정 자세히 보기
분수를 소수로 바꾸면 자릿수 비교가 훨씬 편해집니다.
다음 표를 보면 한눈에 이해할 수 있습니다.
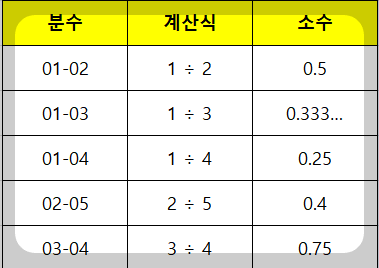
이 표를 활용하면, 분수의 크기를 소수와 직접 비교할 수 있습니다.
예를 들어 0.6과 3/4을 비교하면
3/4 = 0.75이므로, 0.6 < 0.75, 즉 3/4이 더 큽니다.
7️⃣ 무한소수가 나오는 경우
모든 분수가 딱 떨어지는 소수로 바뀌는 것은 아닙니다.
특히, 분모에 2나 5 이외의 수가 들어있을 때는 무한소수가 됩니다.
1/3 = 0.333…
2/3 = 0.666…
1/6 = 0.1666…
이런 경우, 비교를 쉽게 하기 위해 적절한 자리수에서 반올림합니다.
예를 들어 1/3 ≈ 0.33, 2/3 ≈ 0.67 정도로 두고 비교하면 됩니다.
8️⃣ 통분을 이용한 비교도 가능
분수끼리 비교하는 것이 더 익숙한 학생은 소수를 분수로 바꿔서 통분 비교를 하면 됩니다.
소수를 분수로 고친 뒤, 같은 분모를 만들어 분자끼리 비교하는 방식입니다.
예를 들어, 0.4와 3/8을 비교해봅시다.
0.4 = 4/10 = 2/5, 3/8은 그대로 두고
통분하면 2/5 = 16/40, 3/8 = 15/40 → 16/40이 더 큽니다.
따라서 0.4 > 3/8입니다.
9️⃣ 자릿수를 활용한 소수 비교
소수끼리 비교할 때는 자릿수를 맞추는 것이 중요합니다.
예를 들어 0.3과 0.25를 비교할 때,
자릿수를 맞춰서 0.30과 0.25로 보면 됩니다.
0.30 > 0.25이므로 0.3이 더 큽니다.
이 원리는 분수를 소수로 바꿔 비교할 때도 그대로 적용됩니다.
0.5와 0.45를 비교하면 0.50 > 0.45 → 0.5가 더 큽니다.
🔟 실생활 속 예시로 이해하기
분수와 소수의 비교는 실제 생활에서도 자주 쓰입니다.
예를 들어,
A컵에는 1/2리터의 주스가 있고,
B컵에는 0.45리터의 주스가 있다면?
1/2 = 0.5이므로, A컵이 더 많다는 것을 쉽게 알 수 있습니다.
또는
어떤 시험에서 학생 A는 0.75를 맞고,
학생 B는 3/5을 맞았다고 하면,
3/5 = 0.6이므로, A가 더 높은 점수를 받은 셈입니다.
♣ 한눈에 정리하는 비교 방법 요약

🧩 공부할 때 자주 하는 실수
① 분수를 소수로 잘못 계산하는 경우
예: 3/4을 0.34로 착각 → 반드시 나눗셈 계산을 해야 정확함.
② 자릿수 비교를 생략하는 경우
0.3과 0.25를 비교할 때 3과 25만 보고 착각하는 경우 → 자릿수를 맞춰야 함.
③ 무한소수를 반올림하지 않고 그대로 두는 경우
1/3 = 0.333…을 0.3으로 단순화하면 오차가 생김 → 필요한 자리수까지만 반올림.
※ 학습 팁
분수와 소수를 자유롭게 변환할 수 있을 때, 비례식이나 백분율 계산이 훨씬 쉬워집니다.
계산기 없이도 10, 100, 1000 단위 나눗셈 연습을 하면 자동으로 익숙해집니다.
아이들에게는 “분수는 나눗셈이야!”라는 말로 개념을 각인시키면 이해가 빠릅니다.
마무리 정리
분수와 소수의 크기를 비교할 때 핵심은 표현 방식을 통일하는 것입니다.
① 분수를 소수로 바꾸거나
② 소수를 분수로 바꾸어
③ 같은 형태로 만들어 비교해야 합니다.
이 과정을 익히면, 어떤 수가 나오더라도 감으로가 아닌 논리적으로 크기를 판단할 수 있습니다.
분수와 소수는 서로 다른 언어처럼 보이지만, 결국 같은 수를 표현하는 두 가지 방법일 뿐입니다.
이 원리를 이해하면, 수학의 기초 감각이 확실히 다져집니다.