수학의 기초 개념 중 하나인 ‘분수’는 초등학교 3학년 2학기에서 처음 배우는 중요한 단원입니다.
분수는 단순히 수의 형태를 바꿔 표현하는 것이 아니라, 전체 중의 일부를 나타내는 새로운 시각을 길러주는 개념이기도 합니다.
이번 글에서는 초등 3학년 수준에서 꼭 알아야 할 분수의 개념, 종류, 그리고 분수를 이해하는 방법을 자세히 정리해 보겠습니다.
1️⃣ 분수란 무엇일까?
‘분수’는 하나의 전체를 몇 등분했는지와 그 중 몇 개를 취했는지를 나타내는 수입니다.
예를 들어, 피자를 4조각으로 나누고 그 중 1조각을 먹었다면,
전체 중 1조각이므로 ¼(사분의 일)이라고 표현합니다.
전체를 몇 등분했는가? → 분모
그 중 몇 개를 가졌는가? → 분자
📘 예시
- ½ : 전체를 2등분한 것 중 1개 → 전체의 절반
- ⅔ : 전체를 3등분한 것 중 2개 → 전체의 3분의 2
- ¾ : 전체를 4등분한 것 중 3개 → 전체의 4분의 3
이처럼 분수는 전체를 나누어 비교하는 사고력을 키우는 첫걸음입니다.
2️⃣ 분수의 구성 — 분자와 분모
분수는 위아래 두 숫자로 구성되어 있습니다.

윗부분 ‘3’은 분자,
아랫부분 ‘4’는 분모라고 부릅니다.
🧩 분모는 전체를 몇 등분했는지를 알려주고,
🧩 분자는 그 중 몇 개를 가졌는지를 알려줍니다.
즉, 분모는 기준, 분자는 선택된 양이에요.
예를 들어, 3/4는 “전체를 4등분하고 그 중 3조각을 가진 상태”를 의미합니다.
3️⃣ 분수의 세 가지 종류
분수는 분자와 분모의 크기에 따라 세 가지로 나뉩니다.
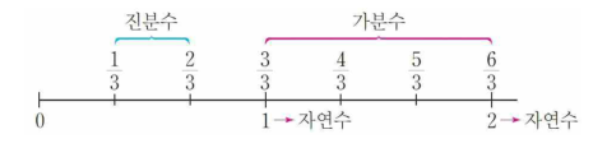
(1) 진분수
분자가 분모보다 작은 분수를 진분수라고 합니다.
즉, 전체보다 작은 양을 나타냅니다.
📘 예시
1/2, 3/4, 2/5, 5/8 등
🍰 설명
케이크를 4조각으로 나누고 3조각만 먹었다면?
→ 전체 케이크보다 적은 양이므로 3/4는 진분수입니다.
👉 진분수는 항상 1보다 작은 수를 나타냅니다.
(2) 가분수
분자가 분모보다 큰 분수를 가분수라고 합니다.
즉, 전체를 모두 초과한 양을 의미합니다.
📘 예시
5/3, 7/4, 9/8 등
🍕 설명
피자를 4조각으로 나누었는데 7조각을 먹었다면?
이미 한 판을 다 먹고, 그 다음 피자의 일부까지 먹은 거예요.
즉, 1보다 큰 양을 의미합니다.
👉 가분수는 실제로는 ‘1과 나머지 분수’로 표현할 수 있습니다.
예를 들어 7/4 = 1과 3/4로 바꿔 쓸 수 있습니다.
(3) 대분수
대분수는 ‘1 이상’의 수를 나타낼 때, 정수와 진분수를 함께 표현한 형태입니다.
📘 예시
1과 2/3, 2와 1/4, 3과 3/5
🧮 설명
1과 2/3은 ‘전체 1개’와 ‘3등분 중 2개’를 더한 수입니다.
즉, 1 + 2/3 = 5/3 (가분수로 바꿀 수 있음)
👉 대분수 ↔ 가분수는 자유롭게 바꿔 쓸 수 있습니다.
4️⃣ 가분수와 대분수의 변환 방법
가분수를 대분수로, 대분수를 가분수로 바꾸는 것은 3학년 수학에서 매우 중요한 포인트입니다.
공식처럼 외우기보다 ‘전체 몇 개 + 남은 조각’으로 이해하면 훨씬 쉽습니다.
🧮 가분수를 대분수로 바꾸기
(예: 7/4)
①분자를 분모로 나눕니다 → 7 ÷ 4 = 1 … 3
②몫은 정수 부분(1), 나머지는 분자(3)
→ 1과 3/4
결과: 7/4 = 1과 3/4
🧮 대분수를 가분수로 바꾸기
(예: 2와 1/3)
①정수 부분(2)을 분모(3)와 곱하기 → 2×3=6
②여기에 분자(1)를 더하기 → 6+1=7
→ 7/3
결과: 2와 1/3 = 7/3
5️⃣ 분수의 크기 비교하기
분수의 크기를 비교할 때는 분모가 같을 때와 다를 때를 구분해야 합니다.
① 분모가 같을 때
분모가 같으면 분자가 큰 쪽이 더 큽니다.
예: 2/5 < 4/5
👉 이유: 전체를 같은 크기로 나눈 상황에서 더 많은 조각을 가진 쪽이 크기 때문입니다.
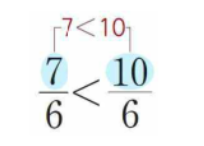
② 분모가 다를 때
이럴 때는 공통 분모(같은 기준)로 바꾸어 비교합니다.
예: 2/3 ? 3/4
→ 2/3 = 8/12, 3/4 = 9/12
따라서 2/3 < 3/4
이 과정을 통해 아이들은 비교 기준의 통일성을 배우게 됩니다.
6️⃣ 생활 속 분수의 예시
분수는 교과서 속 개념이 아니라, 우리 생활 곳곳에 숨어 있는 수학입니다.
- 케이크 한 판 중 절반을 나눠 먹을 때 → 1/2
- 음료를 컵의 3분의 2만 채울 때 → 2/3
- 1m 자에서 4분의 1만큼 재기 → 1/4
- 전기·요리·시간 등에서도 비율로 표현될 때 분수가 사용됩니다.
이런 실생활 예시를 자주 접할수록,
분수는 더 이상 어려운 수학이 아니라 눈에 보이는 개념으로 다가오게 됩니다.
7️⃣ 분수 단원 학습 포인트
그림이나 모형을 이용해 시각적으로 이해시키기
- 분수를 읽고 쓰는 연습을 반복하기
- 분모·분자의 의미를 확실히 구분하기
- 진분수 ↔ 가분수 ↔ 대분수 변환을 직접 해보기
- 실생활 물건으로 직접 분수 나누기 체험
이런 활동 중심 학습은 아이들의 수학 개념 이해력과 수 감각을 함께 길러줍니다.
🌈 마무리하며
분수는 초등 수학에서 단순한 ‘나눗셈의 결과’가 아닙니다.
아이들이 전체 중의 일부를 비교하고, 수를 시각화하는 능력을 기르는 과정이죠.
진분수, 가분수, 대분수의 차이를 이해하는 것은
나중에 비율, 비례식, 소수 등 더 큰 수학 개념을 배우는 밑거름이 됩니다.
분수를 어려워하는 아이들이 많지만,
그림, 음식, 생활 속 도구를 이용해 함께 배우면
“분수는 재미있고, 생활 속에 살아 있는 수학”임을 자연스럽게 깨닫게 됩니다.