수학을 공부하다 보면 더하기, 빼기, 곱하기, 나누기 기호가 함께 들어 있는 ‘혼합 계산식’을 자주 만나게 됩니다.
예를 들어,
12 + 3 × 4
이런 식처럼 여러 연산 기호가 한 문제 안에 섞여 있죠.
이럴 때는 순서대로 차근차근 계산하는 법을 알아야 합니다.
혼합계산은 단순히 계산을 잘하는 것이 아니라, 논리적으로 생각하는 힘을 길러주는 중요한 단원입니다.
이번 글에서는 초등 5학년 수준에 맞게 혼합계산의 원리와 순서를 아주 쉽게 설명해드리겠습니다.
1️⃣ 혼합계산이란 무엇일까?
혼합계산은 이름 그대로 여러 가지 계산이 섞여 있는 계산식을 말합니다.
즉, 더하기(+), 빼기(−), 곱하기(×), 나누기(÷)가 한 식 안에 함께 들어 있는 것이죠.
예를 들어,
24 ÷ 3 + 5 × 2
(15 − 5) × 2
20 ÷ (4 + 1)
이런 식들이 모두 혼합계산에 해당합니다.
2️⃣ 혼합계산의 기본 원칙
혼합계산의 핵심은 ‘계산 순서’입니다.
아무리 숫자와 기호가 많아도, 순서를 잘 지키면 절대 헷갈리지 않습니다.
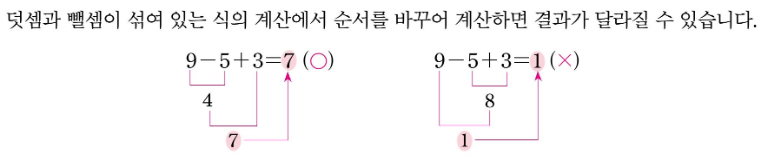
기본 규칙은 다음과 같습니다 👇
① 괄호 안 먼저
② 곱하기와 나누기
③ 더하기와 빼기
이 세 가지만 기억하면 어떤 식이든 정확하게 풀 수 있습니다.
(1) 괄호 안의 계산을 먼저 한다
괄호는 “이 부분을 먼저 계산하세요!”라는 뜻입니다.
괄호가 있으면 무조건 그 안을 가장 먼저 계산합니다.
예를 들어,
10 + (3 × 2)
괄호 안부터 계산하면 3 × 2 = 6,
따라서 전체는 10 + 6 = 16이 됩니다.
괄호가 없다면 곱셈부터 했겠지만, 괄호가 있으므로 순서가 바뀝니다.

(2) 곱하기와 나누기를 먼저 한다
괄호가 없다면, 곱셈(×)과 나눗셈(÷)을 먼저 계산합니다.
예를 들어,
8 + 4 × 3
이 식에서 곱하기를 먼저 계산해야 합니다.
4 × 3 = 12,
그다음 8 + 12 = 20
만약 순서를 지키지 않고 8 + 4를 먼저 계산하면 12 × 3 = 36으로 완전히 다른 답이 나옵니다.
이처럼 순서를 지키는 게 정말 중요합니다.
(3) 더하기와 빼기는 마지막에 계산한다
곱하기와 나누기를 끝낸 뒤에,
남은 더하기(+)와 빼기(−)를 왼쪽에서 오른쪽으로 차례로 계산합니다.
예를 들어,
30 − 5 + 8
이 경우는 곱셈이나 나눗셈이 없기 때문에,
왼쪽부터 순서대로 계산하면 됩니다.
30 − 5 = 25
25 + 8 = 33
(4) 계산이 같은 단계일 때는 왼쪽부터 계산
곱셈이 두 개 나오거나, 나눗셈이 두 개 나오면 왼쪽부터 계산합니다.
더하기, 빼기도 마찬가지입니다.
예를 들어,
36 ÷ 6 ÷ 2
이 경우는 왼쪽부터 계산해야 합니다.
36 ÷ 6 = 6
6 ÷ 2 = 3
만약 오른쪽부터 했다면 36 ÷ (6 ÷ 2) = 36 ÷ 3 = 12로 완전히 달라집니다.
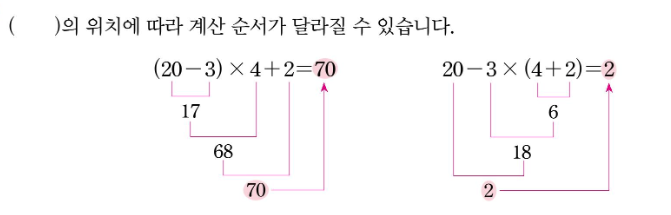
3️⃣ 괄호의 역할 — 순서를 바꾸는 마법
괄호는 계산 순서를 바꾸는 데에 아주 큰 역할을 합니다.
괄호가 하나만 들어가도 전체 식의 결과가 달라질 수 있습니다.
예를 들어,
(6 + 4) × 2 = 10 × 2 = 20
6 + (4 × 2) = 6 + 8 = 14
괄호의 위치에 따라 결과가 완전히 달라집니다.
즉, 괄호는 먼저 계산하라는 표시이자, 계산 순서를 바꾸는 도구입니다.
문제를 풀 때 괄호를 잘못 놓으면 답이 달라질 수 있으니 꼭 주의해야 합니다.
4️⃣ 예제로 배우는 혼합계산
혼합계산의 규칙을 이해했다면,
이제 실제 예제를 통해 차근차근 적용해 보겠습니다.
예제 1
12 + 6 ÷ 3 × 2
순서에 따라 계산하면,
곱하기와 나누기를 먼저 계산
6 ÷ 3 = 2
그다음 2 × 2 = 4
→ 12 + 4 = 16
예제 2
(20 − 8) ÷ 4
괄호 안을 먼저 계산합니다.
20 − 8 = 12
12 ÷ 4 = 3
예제 3
15 − 6 ÷ 3 × 2
곱하기와 나누기를 먼저!
6 ÷ 3 = 2
2 × 2 = 4
15 − 4 = 11
예제 4
(10 + 5) × (6 − 2)
괄호가 두 개 있을 때는 각각 따로 계산합니다.
(10 + 5) = 15
(6 − 2) = 4
15 × 4 = 60
예제 5
24 ÷ (4 + 2) × 3
괄호 안 먼저 계산!
4 + 2 = 6
24 ÷ 6 × 3
→ 24 ÷ 6 = 4
4 × 3 = 12
5️⃣ 혼합계산에서 자주 하는 실수
혼합계산을 어려워하는 이유는 순서를 헷갈리기 때문입니다.
대표적인 실수 유형을 알아두면 계산 실수를 줄일 수 있습니다.
❌ 실수 1. 왼쪽부터 무조건 계산하는 경우
8 + 4 × 3 = 12 × 3 = 36 (오답!)
정답은 곱하기 먼저 → 4 × 3 = 12 → 8 + 12 = 20
❌ 실수 2. 괄호 무시하기
(12 − 2) × 3 = 10 × 3 = 30 (정답)
괄호 무시 → 12 − 2 × 3 = 12 − 6 = 6 (오답)
괄호가 있으면 반드시 먼저 계산해야 합니다.
❌ 실수 3. 나눗셈 방향 헷갈리기
36 ÷ 6 ÷ 2
왼쪽부터 계산해야 하므로 36 ÷ 6 = 6, 6 ÷ 2 = 3
오른쪽부터 하면 완전히 다른 답이 됩니다.
6️⃣ 혼합계산을 잘하려면
혼합계산은 단순히 암기만으로는 잘 풀 수 없습니다.
문제를 읽고 계산 순서를 스스로 판단하는 연습이 중요합니다.
아래 방법으로 연습해 보세요 👇
㉮ 식의 구조를 먼저 파악하기
괄호가 있는지, 곱셈·나눗셈이 있는지 눈으로 확인합니다.
㉯계산 순서를 번호로 표시하기
①, ②, ③ 표시를 해두면 헷갈리지 않습니다.
㉰ 머릿속으로 식을 ‘단계별로 정리’하기
예: “먼저 나누기, 그다음 곱하기, 마지막 더하기.”
㉱ 검산(다시 계산하기) 습관 들이기
다른 순서로 계산해도 결과가 같아야 정답입니다.
7️⃣ 혼합계산이 중요한 이유
혼합계산은 단순히 수학 문제를 푸는 기술이 아니라,
논리적 사고력과 문제 해결력을 키워주는 기본 훈련입니다.
실제로 중학교 이후 수학에서는
식 변형, 방정식, 함수 등 복잡한 계산을 할 때
‘계산 순서’를 정확히 지키는 것이 매우 중요합니다.
즉, 혼합계산을 잘 이해하면
나중에 어려운 수학 문제도 훨씬 쉽게 풀 수 있게 됩니다.
✅ 정리
계산 단계 내용 예시
① 괄호 안 먼저 계산 (6 + 4) × 2
② 곱하기, 나누기 8 + 4 × 3 → 8 + 12
③ 더하기, 빼기 30 − 5 + 2 = 27
④ 같은 단계는 왼쪽부터 36 ÷ 6 ÷ 2 → 3
마무리
혼합계산은 초등 5학년 수학의 핵심 단원입니다.
하지만 규칙만 정확히 기억하면 전혀 어렵지 않습니다.
“괄호 → 곱하기·나누기 → 더하기·빼기”
이 순서를 머릿속에 새기세요.
그리고 문제를 풀 때는 언제나 차근차근 순서대로 풀면 됩니다.
그 습관이 바로 수학 실력을 키우는 첫걸음입니다.